Cryptology 암호학
암호학은 크게 두 분야로 나눌 수 있다. 암호를 제작하는 분야와 만들어진 암호를 해독하기 위한 분야가 그 것이다.
암호학(cryptology)
- Cryptography : 암호의 구축과 작성을 위한 암호학 분야.
- Cryptanalysis : 암호를 분석하여 해독하기 위한 암호학 분야.
암호 사용의 Model
평문(plain text): 아직 암호화 되지 않은 원문.
암호문(cipher text): 평문이 암호화(encryption) 과정을 거쳐 암호화된(ciphered) 결과
암호화(encryption): 평문을 암호문으로 바꾸는 과정.
복호화(decryption): 암호문(cipher text)을 평문(plain text)으로 되돌리는 과정.
암호화 키(encryption key): 평문을 암호문으로 변경하기 위한 비밀번호(key).
복호화 키(decryption key): 암호문을 평문으로 복원하기 위해 사용하는 비밀번호(key).
암호 사용 모델:
평문 ------> 암호문 =========> 암호문 --------> 평문
암호화 통신 복호화
암호화는 통신의 발신자(송신자, sender)가 실행하는 내용이고,
복호화는 통신의 수신자(receiver)가 원문으로 복원하기 위하여 실행하게 된다.
참고: 복호화 과정은 수신자가 정당하게 암호문을 평문으로 복원하는 것을 의미하는 한편, 암호분석(cryptanalysis)는 중간에서 가로챈(예를 들면, 도청 등을 통하여) 암호문을 복호화 키가 없이 평문으로 복원하려는 시도 및 과정을 의미한다.
암호의 필요성
정보통신의 발달과 함께, 정보의 소통량과 전달, 이동 등의 양이 급증하게 되었다. 또한 소통되는 정보의 내용도 사무자동화와 함께, 군사기밀, 정부정책문서, 사업기밀 등 중요한 내용 등을 포함하게 되었다. 그러므로, 정보를 보내는 발신자와 정보를 받아보는 수신자 모두 도청(eavesdropping)을 당하지 않기 위해 비밀번호(key, 키)를 사용하여 발신 원문을 암호문으로 바꾸어 전송하고 수신자는 수신된 암호문을 복원하여 평문으로 고치는 과정을 필요로 하게 되었다.
인터넷 등의 발달로 전자상거래 등이 보편화되고 사업형태도 변모하게 되어 암호학의 사용은 더욱 중요도를 높여가고 있으며, 국내에서의 암호학의 발전도 시급한 실정이다. 암호를 이용한 응용을 살펴보면,
- 전자상거래(electronic business): 인터넷을 이용한 전자 신용 상거래.
- 전자 인증(authentication): 인터넷 등 통신을 이용한 인증체계.
- 디지털 서명(digital signature): 통신을 이용한 서명 방식.
- 전자 화폐(electronic money, digital money, cyber cash, virtual currency 등): 통신에 의한 전자상거래에서 사용할 수 있는 가상 화폐.
이 외에도 스마트 머니 등 다양한 암호화가 필요한 통신 대상 들이 급증하고 있고, 상업 형태도 급변하고 있는 실정이다.
암호의 종류
시대별 구분
- 고전암호 (약 기원전 400년 ~ 1920년경): 대입암호, 치환암호 등 일상적으로 사용하는 글자, 단어 등을 단순히 다른 기호로 대치하는 형태의 암호. 시이저(Caesar)가 처음 사용한 것으로 알려져 있음.
- 기계암호 (1920 ~ 1950): 세계대전을 치루는 기간 동안의 시기에 전쟁을 위한 군사기밀의 통신을 위한 암호의 사용으로 발달한 암호. 특히, 독일이 암호화를 위한 기계장비를 개발한 것이 암호학 발달에 큰 영향을 미침. 또 그에 반하여, 암호의 해독기술도 따라 발달하게 됨.
"도라,도라,도라" 등 암호분석에 의하여 전쟁을 승리한 내용을 영화화한 영화도 제법 많이 있음. - 현대암호: 기계식 암호의 해독도 컴퓨터의 발달과 함께 용이해져서 수학적 어려움을 이용한 암호의 형태로 변형됨. 대표적인 현대암호로 DES암호와 RSA암호가 있음.
기능별/형태별 구분
- 대칭암호(symmetric cipher):
암호화 키와 복호화 키가 같은 암호체계. 두 개의 키(key)가 같으므로 원하지 않는 사람에게로의 키의 유출을 막기 위하여서는 키를 비밀리에 사용하여야 함. 그래서 비밀키 암호(secret key cipher)라고도 함.
대표적인 암호로 DES 암호가 있음. - 비대칭암호(asymmetric cipher):
암호화 키가 복호화 키와는 다른 암호체계. 그러므로, 암호화 키는 공개하여도 도청의 염려가 없음. 그래서 공개키 암호(public key cipher)라고도 함. 전자상거래 등에 이용됨.대표적 암호로 RSA 암호가 있음.
암호의 분석/공격/해독
암호의 해독을 위한 공격법으로
- 전수공격(keyexhaustion): 가능한 모든 키를 실행해보는 암호해독방법.
- 통계적분석(statistical analysis): 통계적으로 개연성이 큰 키를 만들어내는 암호해독법.
- 수학적분석법(mathematical analysis): 가장 전문적인 암호해독 방법. 이는 암호학의 발달로 인해 암호가 수학문제와 이론 등을 이용하여 제작되었기 때문에 해독법의 개발을 위해서는 수학적 이론이 필요하게 된 탓.
DES 알고리즘
- 컴퓨터와 통신기술의 발달로 인해 암호의 사용이 불가피하게 됨.
- 1973년 5월, 미국의 NBS(National Bureau of Standards, 국립 표준국)가 document의 저장과 전송 등을 위한 암호 알고리즘을 공모.
- 1975년, IBM(Internation Business Machines, Inc. 아이비엠)의 연구원 W. Tuckman 과 C. Meyer 가 DES(Data Encryption Standard) 암호 알고리즘을 제안.
- 1976년 IBM이 지적소유권을 포기.
- 1977년 1월 NSA(National Security Agency)의 검토를 거쳐 NBS가 DES를 표준 암호 알고리즘으로 선정함.
- 매 5년마다 재인증. 1983년과 1994년 재인증을 받아 표준 암호로 건재하게 사용되고 있음.
* DES 암호는 그 내용을 공개하여 <암호학의 발달>을 가져오고 또한 컴퓨터의 발달에 따라 DES를 대신할 알고리즘 개발이 한창 진행 중임.
RSA 공개 키 암호
1976년, Diffie & Hellman 이 공개키암호의 사용을 제안.
1978년, MIT 교수 Rivest, Shamir, Adleman 등 3명은 블록암호로서 공개키 암호를 개발. 그들의 이름을 따서 RSA 암호로 지칭함.
RSA 암호는 기본적인 정수론을 이용한 암호로 가장 널리 사용되고 있다.
- 인수분해.
- 합동.
- Euler 함수.
- Euler 정리( 또는 Fermat 정리).
인수분해 (Prime Factorization)
합동 (Congruence)
임의의 2 개의 정수 a 와 b 가 정수 n을 기준으로 서로 합동이다
<=> a 와 b 는 n으로 나누었을 때 나머지가 같다.
<=> a - b = n 의 배수 = q. n for some integer q.
<=> 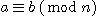
<=> a and b are congruent to each other modulo n.
예제: 만약 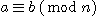 이고
이고 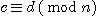 이라면,
이라면,
(1) 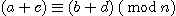 이다.
이다.
(2) 임의의 정수 k 에 대하여, 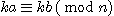 이다.
이다.
(3) 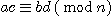 이다.
이다.
(4) 심지어, f(x)를 다항식이라고 할 때, 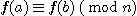 임도 성립한다.
임도 성립한다.
Euler 함수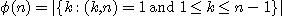
즉, 오일러 함수는 자기 자신 미만의 자연수 중에 자신과 서로 소인 자연수의 개수를 의미.
예제: (1) p 가 소수라면, 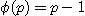 .
.
(2) p, q 가 소수라면 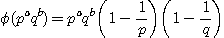 .
.
(3) 특히, 위의 식에서 a=1, b=1 이라면 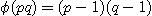 이다.
이다.
Euler 정리
서로소인 임의의 정수 a 와 n 에 대하여, 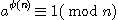 이 성립한다.
이 성립한다.
예제: n=6, a=35 일 때, 위의 Euler 정리가 성립함을 보여라.
Fermat 정리
p 는 소수이고, a 는 p 와 서로소인 정수이다. 그러면 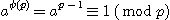 가 만족된다. 다시 말해,
가 만족된다. 다시 말해, 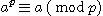 이다.
이다.
위의 Fermat 정리는 오일러 정리의 특수한 경우이고, 이를 이용하여 RSA 암호를 제작하였다.
예제: p=7, a=9 라고 하고, 페르마 정리가 성립함을 보여라.
정리. p 와 q 는 소수이다. 또 정수 d 와 e 가 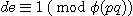 를 만족하는 정수이다. 그러면, 임의의 정수 M은
를 만족하는 정수이다. 그러면, 임의의 정수 M은 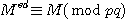 가 된다.
가 된다.
이 정리의 증명은 페르마 정리 또는 오일러 정리를 이용하여 하고, RSA 암호는 이 정리의 원리를 이용하여 제작된다. 위 정리는 3개의 정수가 사용되는데, 하나는 pq, 다른 두 개는 e 와 d 이다. 이 때 RSA암호는 n=pq 와 e 의 두 개의 정수를 공개키로 사용하고, 정수 d를 비밀키(복호화를 위한 키)로 사용한다. 정수 M 은 평문에 해당하고, M을 e 번 곱한 값 Me 가 암호문이 되는 것이다. 수신자는 암호문에 해당하는 수를 다시 d 번 곱하면 위 정리에 의하여 M을 복원하게 된다. 이 것이 RSA 암호의 원리이다.
RSA 암호에 사용되는 키
|
공개키(public key, 암호화 키로 사용) |
비밀 키(secret key, 복호화 키로 사용) |
|
n = pq 여기서 p 와 q 는 소수 |
d, 복호화 키 |
예제: p=41, q=53 이라 하자. 그러면 n=p x q=41 x 53=2173.
2173의 오일러 함수 값은 Φ(2173)=Φ(41 x 53)=(41-1)(53-1)=2080.
여기서, 또, e=207, d=623 이라 하자. 그러면 de=623 x 207≡1(mod 2080)이 됨.
그러면, M을 평문이라 하면, Med≡M 이 되어 Me를 M의 암호문으로 사용한다.
'Cryptography' 카테고리의 다른 글
| 암호화 및 키관리 PDF파일 (0) | 2012.07.09 |
|---|---|
| 암호학 수업1일차 (0) | 2012.07.02 |
| 암호학 (0) | 2012.07.02 |
 암호학.ppt
암호학.ppt